Cartes de contrôle pour les données alternatives (attributs, décomptes) p-chart, np-chart, C-chart et u-chart ou une carte XmR de valeurs individuelles ?
"La difficulté liée à l'utilisation des graphiques p, np, C ou u est qu'il est difficile de déterminer si les modèles binomiaux ou de Poisson sont appropriés pour les données."
Nous présentons une traduction de l'article de Donald Wheeler : « Qu'en est-il de la carte p ? Quand devez-vous utiliser les cartes de contrôle p-chart, np-chart, C-chart et u-chart pour des données alternatives (comptes) ? / Donald J. Wheeler, Article : « Qu'en est-il des p-Charts ? Quand devrions-nous utiliser les graphiques spécialisés p-chart, le np-chart, le c-chart et le u-chart pour les données de comptage ? [31]
Traduction et notes : Directeur scientifique du Centre AQT Sergueï P. Grigoriev .
Le libre accès aux articles ne diminue en rien la valeur des matériaux qu'ils contiennent.
Contenu
Toutes les cartes de contrôle basées sur les données de comptage sont des cartes de valeurs discrètes. Que nous travaillions avec des quantités ou des fractions, nous recevons une valeur par période de temps et souhaitons tracer un point sur le graphique chaque fois que nous recevons une valeur. C'est pourquoi quatre cartes de contrôle spécifiques ont été développées pour les données basées sur le comptage, avant même la découverte de l'approche de construction de cartes de contrôle XmR de valeurs individuelles et de plages mobiles. Ces quatre types de cartes de contrôle sont la p-card, la np-card, la C-card et la u-card. Cet article demande quand utiliser ces cartes de contrôle et d'autres cartes de contrôle spéciales avec des données basées sur le nombre.
La première de ces cartes de contrôle spéciales, la carte p, a été créée par Walter Shewhart en 1924. À cette époque, l'idée d'utiliser une plage mobile à deux points pour mesurer la dispersion d'un ensemble de valeurs individuelles avait pas encore surgi (W. J. Jennett a proposé cette idée en 1942). Le problème auquel Shewhart était donc confronté était de savoir comment créer un diagramme de comportement de processus pour des valeurs discrètes basées sur des comptes. Bien qu'il puisse tracer les données comme un enregistrement actuel et bien qu'il puisse utiliser la moyenne comme ligne centrale pour cet enregistrement actuel, l'obstacle était de savoir comment mesurer la variance pour filtrer les variations normales. Avec des valeurs discrètes, il ne voyait aucun moyen d'exploiter la variation au sein d'un sous-groupe, mais il savait qu'il valait mieux ne pas essayer d'utiliser une statistique d'écart type global, qui serait gonflée par toute variance exceptionnelle dans les données disponibles. Il a donc décidé d’utiliser des limites de contrôle théoriques basées sur un modèle probabiliste.
Les modèles probabilistes classiques pour les données de dénombrement simples sont binomiaux et Poisson, et Shewhart savait que ces deux modèles avaient un paramètre de variance fonction de leur paramètre de localisation. Cela signifiait que l'estimation de la moyenne obtenue à partir des données pouvait également être utilisée pour estimer la variance. Ainsi, avec les seules statistiques de localisation, il pouvait estimer à la fois la ligne centrale et la distance trois sigma.
Figure 1 : Cartes de contrôle spéciales de Shewhart pour ces calculs.
Cette double utilisation de la moyenne pour caractériser à la fois l'emplacement et la variance signifie que les cartes p, np, C et u ont des limites de contrôle basées sur la relation théorique entre la moyenne et la variance.
Par conséquent, on peut dire que toutes les cartes de contrôle spéciales utilisent des limites de contrôle théoriques. Si les décomptes peuvent être raisonnablement modélisés à l'aide d'une distribution binomiale ou d'une distribution de Poisson, alors des limites de contrôle appropriées peuvent être obtenues pour les graphiques de valeurs discrètes.
Ces dernières années, de nombreux manuels et normes ont oublié que l'hypothèse d'un modèle binomial ou de Poisson est une exigence primordiale pour l'utilisation de ces cartes de contrôle spéciales. Cela pose un problème car il existe de nombreux types de données basées sur les décomptes qui ne peuvent être caractérisées comme des distributions binomiales ou de Poisson. Lorsque vous placez ces données sur une carte p, une carte np, une carte C et une carte u, les limites de contrôle théoriques qui en résulteront seront incorrectes.
Alors, que devrions-nous faire? Le problème avec les limites de contrôle théoriques réside dans l’hypothèse selon laquelle nous connaissons la relation exacte entre la ligne centrale et la distance trois sigma. La solution consiste à obtenir une estimation distincte de la variance, ce que fait la carte XmR : tandis que la moyenne caractérisera l'emplacement et servira de ligne centrale pour la carte X des valeurs individuelles, la plage moyenne mobile de la carte mR caractérisera la variance et servira de base pour calculer la distance à trois sigma pour la carte X.
Ainsi, la principale différence entre les cartes de contrôle de comptage dédiées et la carte XmR des valeurs individuelles et des plages mobiles réside dans la manière dont la distance trois sigma est calculée. Les cartes p, np, C et u de référence auront la même entrée actuelle et essentiellement les mêmes axes que la carte X. Mais lorsqu'il s'agit de calculer les limites de contrôle trois sigma, les cartes de contrôle dédiées utilisent la relation théorique estimée pour calculer les valeurs théoriques, tandis que la carte XmR mesure réellement la variation présente dans les données et construit des limites de contrôle empiriques.
Pour comparer les cartes de contrôle personnalisées avec la carte XmR, nous utiliserons trois exemples. Le premier utilisera les données présentées dans la figure 2. Ces valeurs proviennent du service comptable, qui suit le nombre de comptes clôturés « à temps » chaque mois. Les décomptes indiqués représentent le nombre mensuel de fermetures qui ont été complétées à temps pour 35 fermetures (zone de définition égale).
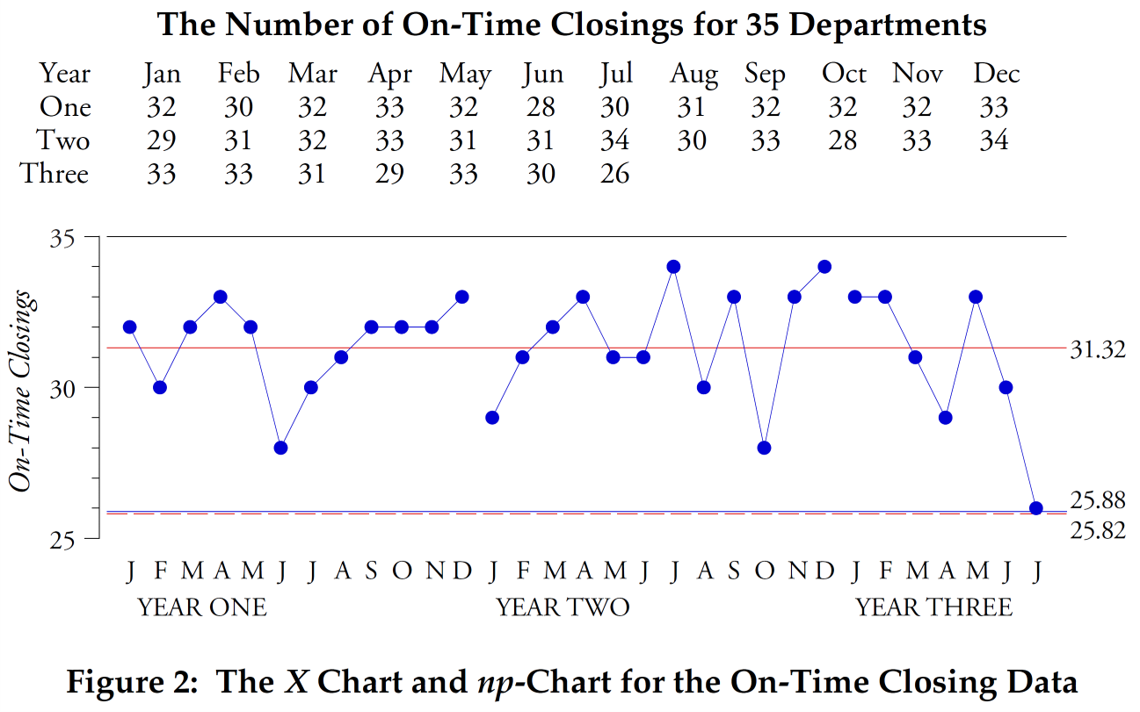
Riz. 2 : X-card et np-graph du nombre mensuel de comptes clôturés à temps sur 35 comptes.
Les lignes pointillées rouges représentent les limites de contrôle supérieure et inférieure pour la carte X, et bleues pour la carte P.
Ici, les calculs pour le np-chart et la X-map des valeurs individuelles donnent des limites de contrôle presque identiques (la limite de contrôle supérieure de 36,8 n'est pas affichée car elle dépasse la valeur maximale de 35 fermetures à temps). Ici, les deux approches sont essentiellement identiques car ces décomptes semblent être modélisés de manière appropriée par la distribution binomiale. Si vous êtes suffisamment compétent pour reconnaître quand cela se produit, vous saurez alors quand la carte np fonctionnera et pourrez l'utiliser avec succès. D'un autre côté, si vous n'êtes pas suffisamment expérimenté pour savoir quand le modèle binomial est approprié, vous pouvez toujours utiliser la carte XmR. Comme on peut le voir ici, lorsque la carte np fonctionnerait, les limites de contrôle empiriques de la carte X seraient identiques aux limites de contrôle théoriques de la carte np, et vous ne perdriez rien en utilisant la carte XmR au lieu du np-graphique.
Dans notre prochain exemple, nous utiliserons les livraisons à temps pour une usine. Les données sur le pourcentage de livraison à temps par mois sur deux ans sont présentées dans la figure 3, accompagnées d'une carte X des valeurs individuelles et d'un graphique P pour ces données.
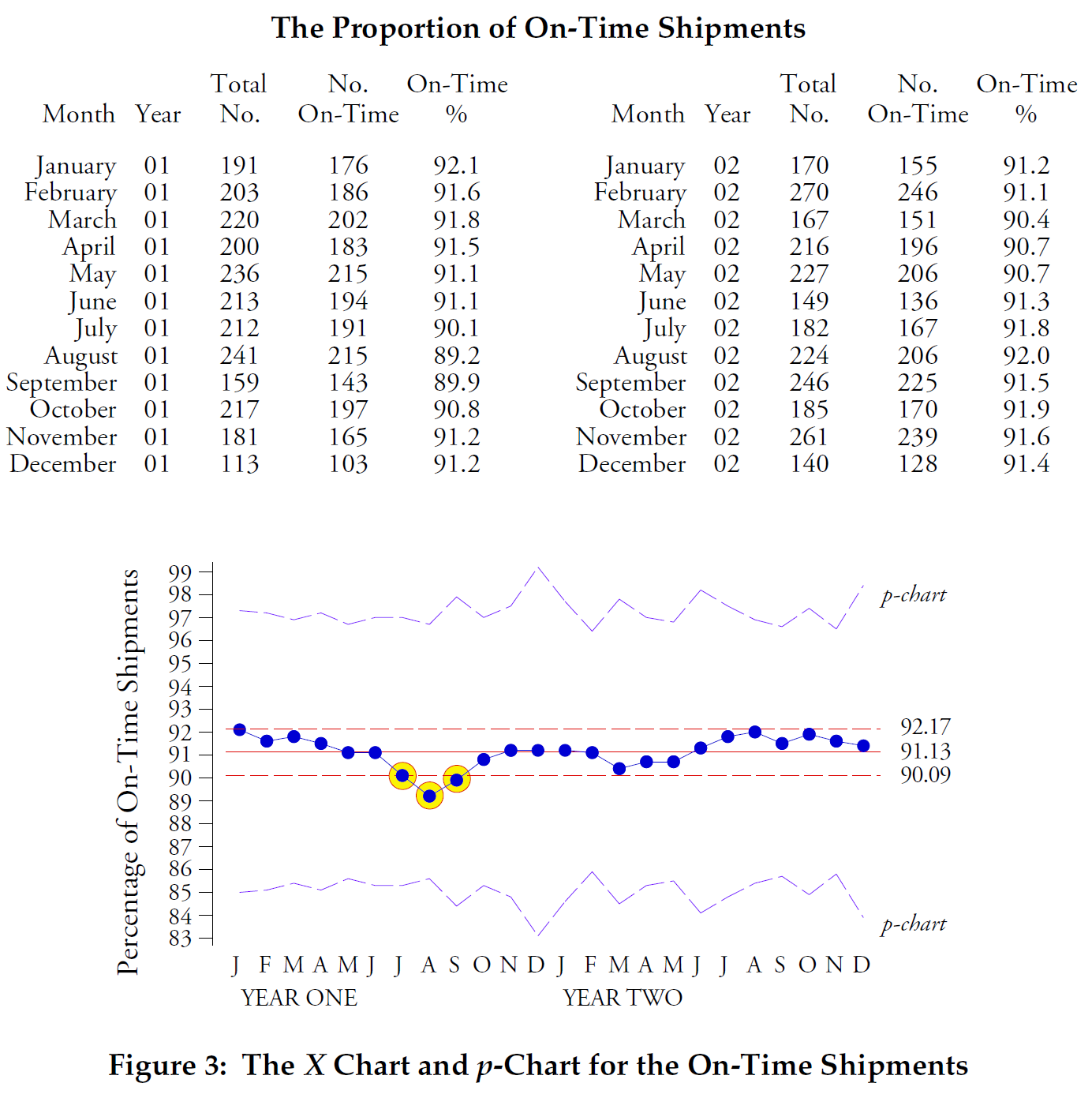
Figure 3 : X-map et p-chart pour le pourcentage de livraison à temps par mois sur deux ans.
La carte X montre un processus avec trois points égaux ou inférieurs à la limite de contrôle inférieure. Les limites de contrôle de la carte P à largeur variable sont cinq fois plus larges que les limites de contrôle de la carte X trouvées à l'aide de travées glissantes. Aucun point ne dépasse ces limites de contrôle de la carte P. Cet écart entre les deux ensembles de limites de contrôle indique que les données de la figure 3 ne satisfont pas aux conditions binomiales. En particulier, la probabilité qu’un envoi arrive à temps n’est pas la même pour tous les envois au cours d’un mois donné. Étant donné que le modèle binomial n’est pas adapté à ces données, les limites théoriques de contrôle de la carte P sont incorrectes. Cependant, les limites de contrôle empiriques de la carte XmR, qui ne dépendent pas de l'ajustement d'un modèle probabiliste particulier, sont correctes.
Notre comparaison finale utilisera les données de la figure 4. Nous avons ici le pourcentage des expéditions entrantes pour une usine d'assemblage électronique qui ont été expédiées par fret aérien. Deux points se situent en dehors des limites de contrôle de la carte P à largeur variable, mais aucun point ne se situe en dehors des limites de contrôle de la carte X.
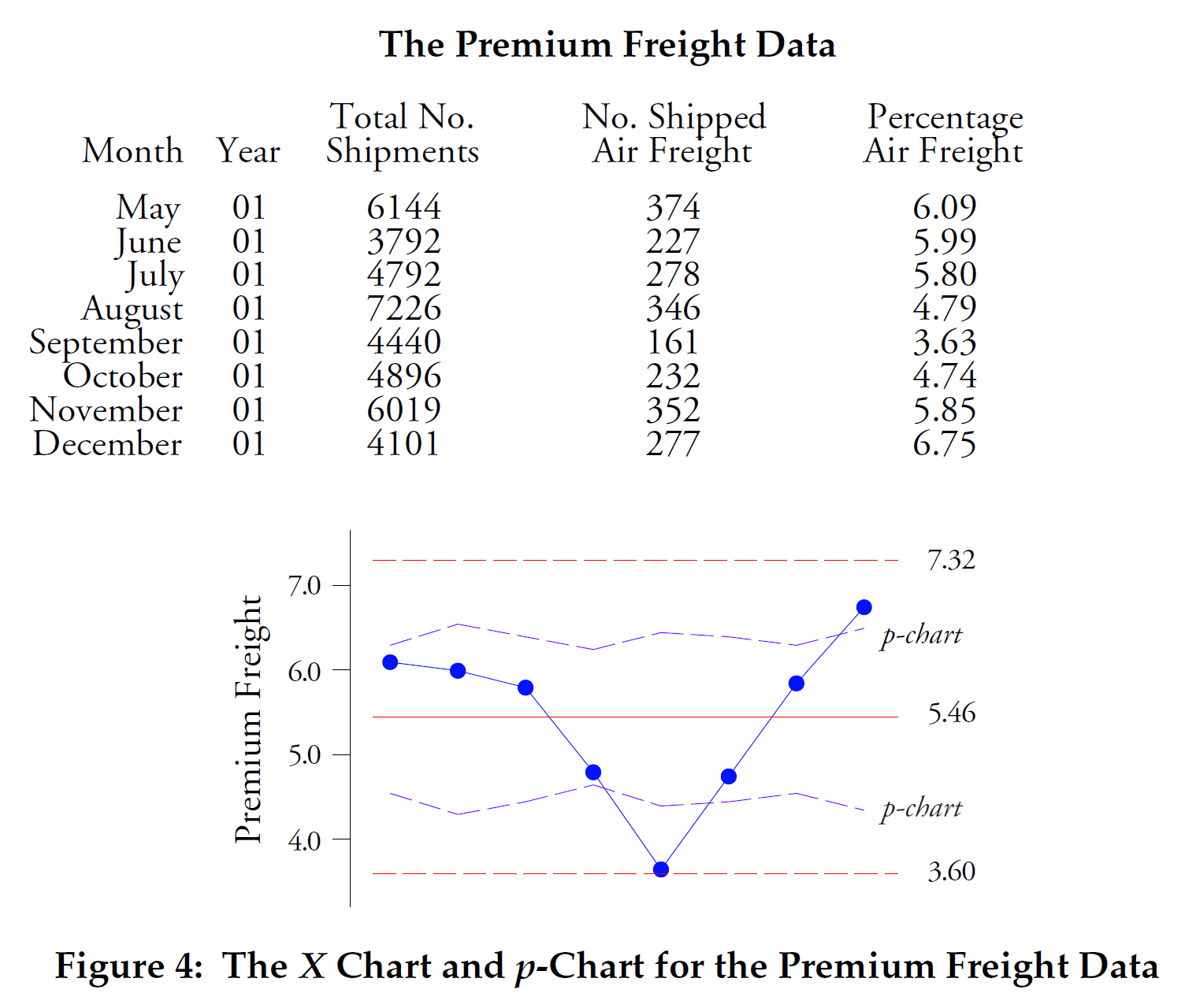
Figure 4 : Carte X des valeurs individuelles et graphique P pour le pourcentage d'expéditions utilisant le fret aérien.
La figure 4 est typique de ce qui se passe lorsque la « zone d'opportunité » de compter des objets devient excessivement grande. Le modèle binomial exige que tous les éléments d’une période donnée aient une chance égale de posséder l’attribut pris en compte. Cette exigence n'est pas remplie ici. Avec des milliers d’envois chaque mois, la probabilité qu’un envoi soit envoyé par voie aérienne n’est pas la même pour tous les envois. Ainsi, le modèle binomial n’est pas adapté et les limites théoriques de contrôle de la carte P qui dépendent du modèle binomial sont incorrectes. Les limites de contrôle de la carte X, qui sont ici deux fois plus larges que les limites de contrôle de la carte p, caractérisent correctement à la fois l'emplacement et la répartition de ces données et constituent les limites de contrôle correctes à utiliser.
Ainsi, la difficulté liée à l’utilisation des diagrammes p, des diagrammes np, des diagrammes C ou des diagrammes en u est qu’il est difficile de déterminer si les modèles binomiaux ou de Poisson sont appropriés pour les données. Comme vous pouvez le constater sur les figures 3 et 4, si vous ne remplissez pas les conditions principales des cartes de contrôle spéciales, vous risquez de commettre une grave erreur en pratique. C'est pourquoi vous devez éviter d'utiliser des cartes de contrôle ad hoc à moins de savoir comment évaluer l'ajustement des données à ces modèles probabilistes.
Contrairement aux modèles théoriques qui peuvent être corrects ou non, la carte XmR nous fournit des limites de contrôle empiriques qui sont en réalité basées sur la variation présente dans les données. Cela signifie que vous pouvez utiliser le graphique XmR avec des données basées sur le nombre à tout moment. Étant donné que les graphiques p, np, C et u sont des cas particuliers de graphiques à valeurs discrètes, le graphique XmR imitera ces graphiques spéciaux lorsqu'ils sont appropriés et en différera en cas d'échec.
Dans le cas de cartes de contrôle spéciales ayant des limites de contrôle de largeur variable, le XmR-cut simulera les limites de contrôle en fonction de la zone de définition moyenne des cartes de contrôle pour les comptages. De plus, lorsque je fais ces comparaisons, je préfère avoir au moins 24 comptes dans la période de base.
Figure 5 : Approche sans hypothèse pour les données basées sur le nombre.
Ainsi, si vous n'avez pas de diplôme supérieur en statistiques, ou si vous avez simplement du mal à déterminer si vos décomptes peuvent être caractérisés par une distribution binomiale ou de Poisson, vous pouvez toujours tester votre choix d'un graphique spécial pour votre décompte. données en comparant les limites de contrôle théoriques avec les limites de contrôle empiriques de la carte XmR. Si les limites de contrôle empiriques sont approximativement les mêmes que les limites théoriques, alors le modèle probabiliste fonctionne. Si les limites de contrôle empiriques ne correspondent pas aux limites de contrôle théoriques, alors le modèle probabiliste est incorrect.
Vous pouvez toujours être sûr que vous disposez des limites de contrôle correctes pour vos données basées sur le comptage si vous utilisez une carte XmR dès le départ. L’approche empirique sera toujours correcte.
Remarque (S. Grigoriev)
Dans son livre « Contrôle statistique des processus. Business Optimization Using Shewhart control charts », Donald Wheeler définit une autre condition nécessaire pour minimiser l'impact de la discrétion des données de calcul sur les limites de contrôle empiriques de la carte XmR des valeurs individuelles :
"Une carte XmR pour les données discrètes peut être construite dans tous les cas où la valeur de comptage moyenne est supérieure à un. Si elle est supérieure à deux, alors l'effet de la discrétion sur les limites de contrôle sera négligeable.
Puisqu’il est rarement judicieux d’utiliser des quantités discrètes lorsque des résultats de mesure peuvent être obtenus, l’utilisation d’attributs est généralement limitée aux situations dans lesquelles les erreurs peuvent être comptées. Cependant, définir une « erreur » est généralement extrêmement difficile.
La principale difficulté dans la définition d’une « erreur » est le problème définitions opérationnelles ".
Ainsi, si vous avez une moyenne des comptes par domaine de définition inférieure à deux, vous pouvez facilement neutraliser ce problème en augmentant le domaine de définition pour obtenir la moyenne des comptes à une valeur égale ou supérieure à 3 (trois), ce qui C'est particulièrement vrai pour les événements à distribution de Poisson (on compte les défauts, pas les produits défectueux, et seuls les défauts peuvent être comptés, mais en aucun cas le nombre de « non-défauts »).
Par exemple
Si vous avez un nombre moyen de défauts par zone de définition égal à un mètre carré de tissu égal à 1 (un), vous pouvez utiliser une zone de définition de trois mètres carrés, obtenant un nombre moyen de défauts par nouvelle zone de définition égale à 3 (trois) mètres carrés. Utilisez la zone de définition que vous pouvez facilement sélectionner pour vérifier (tester), par exemple, pour un rouleau de tissu de 1,2 mètre de large, vous pouvez utiliser une zone de définition de 3 mètres linéaires.
Formule de calcul du domaine de définition minimum requis :
Si la moyenne des données historiques est < 3, alors
le nouveau domaine minimum de définition est obtenu en multipliant le domaine de définition actuel par un coefficient (k) :
k = 3/valeur moyenne des décomptes de données historiques ;
nouveau domaine minimum = k × domaine actuel.
Sélectionnez le domaine de définition (=) ou (>) du nouveau domaine de définition minimum résultant qui convient au contrôle.
Pour les valeurs binomiales (oui/non, défectueux/non défectueux, pas à l'heure/à l'heure), vous pouvez utiliser le graphique XmR pour les valeurs des résultats positifs plutôt que négatifs, comme implémenté dans les exemples 1 (Figure 2) et 2 (Figure 3) de cet article de Donald Wheeler. L'effet de la discrétion des données du modèle binomial sur le graphique XmR des valeurs individuelles suit les mêmes règles que pour les modèles de Poisson, gardez la moyenne des comptes de résultats (oui/non) à au moins trois (3).
Attention!
Si les étendues sont différentes, vous ne pouvez pas comparer les décomptes sans les convertir en fractions des étendues correspondantes. S'il vous est encore difficile d'interpréter les actions, vous pouvez ramener les valeurs de calcul obtenues à un seul domaine de définition, comme dans l'exemple 1 de cet article de D. Wheeler en utilisant l'exemple d'une carte de contrôle de fermeture en temps opportun comptes. Pour ce faire, vous pouvez utiliser la formule ci-dessous.
Qu'est-ce que tu cherches:
X je - le nombre de coups réduit à un domaine de définition constant.

« Toutes les fractions sont des fractions, mais toutes les fractions ne sont pas des fractions. Une fraction peut être considérée comme une fraction lorsque le dénominateur décrit le domaine de définition des valeurs du numérateur.
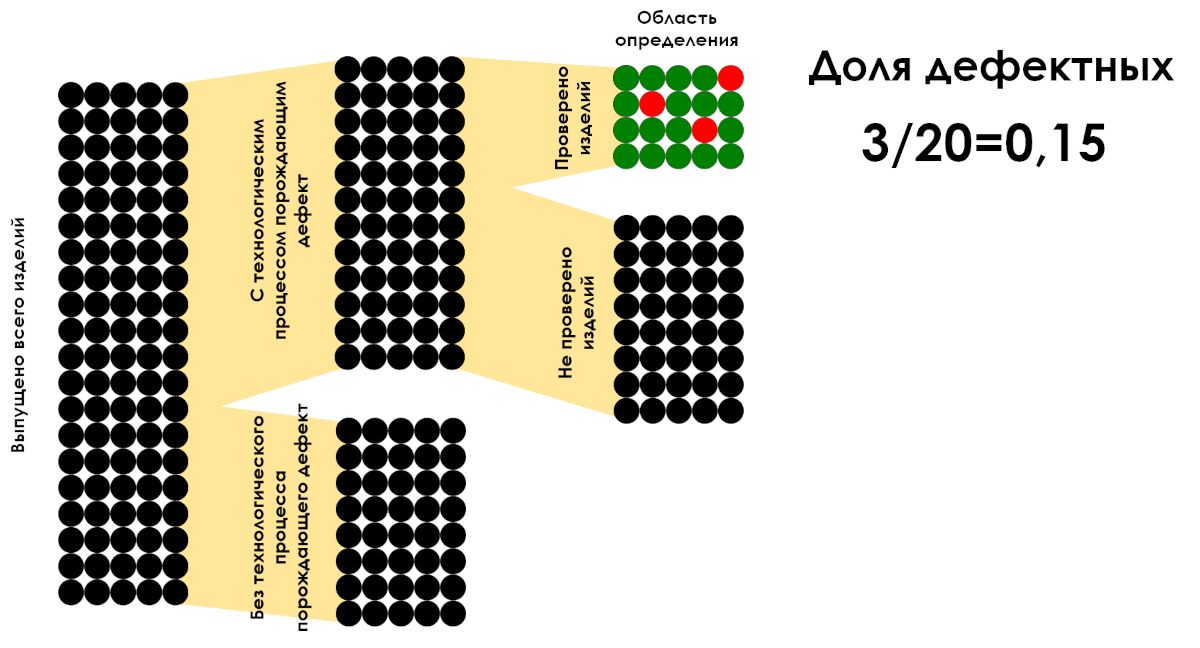
Figure 6 : Exemple de calcul de la proportion de produits défectueux par zone de définition. Seul le rapport 3/20 est une fraction.
Vous devez veiller à suivre toutes les recommandations de cet article au stade de la planification collecte de données. Dans la grande majorité des cas, si les données ne représentent pas le résultat d’un contrôle à 100 %, toute manipulation des données historiques disponibles pour élargir la portée de la définition à l’aide des mathématiques déformera l’image de ce qui se passe.